作为理工科学生,大家或多或少都听过梯度下降法、牛顿法、粒子群算法这类名词,却又极可能理不清它们之间的关系。
无论是求解复杂的非线性方程(组),处理最优化问题,还是训练机器学习模型,都需要借助这些最优化算法来实现。或许实现途径不同,但是它们的共性都是:
研究在给定约束之下如何寻求某些因素,以使某一指标达到最优。
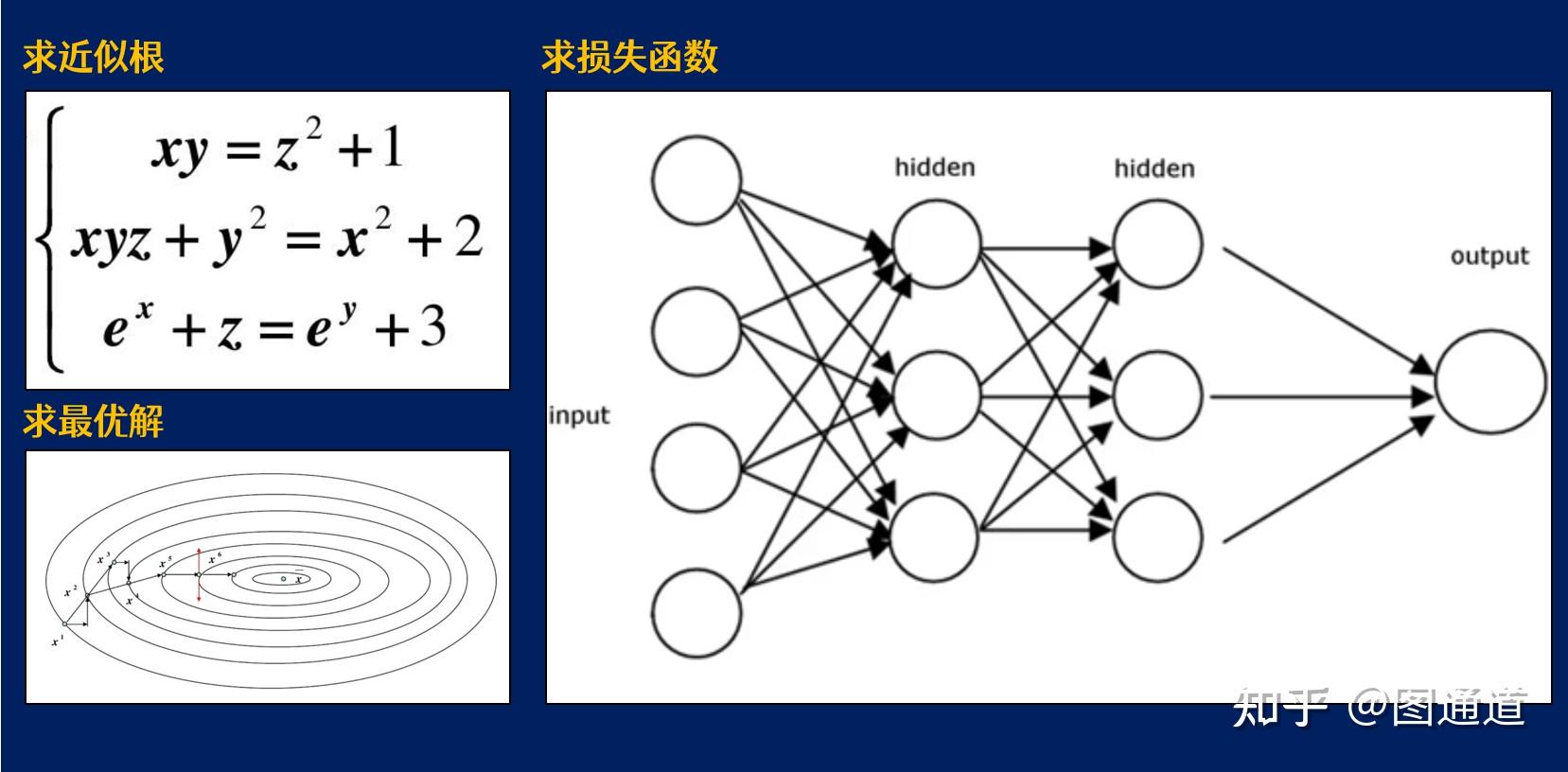
梯度下降法利用函数的一阶泰勒展开作为函数的近似,即用直线近似曲线。
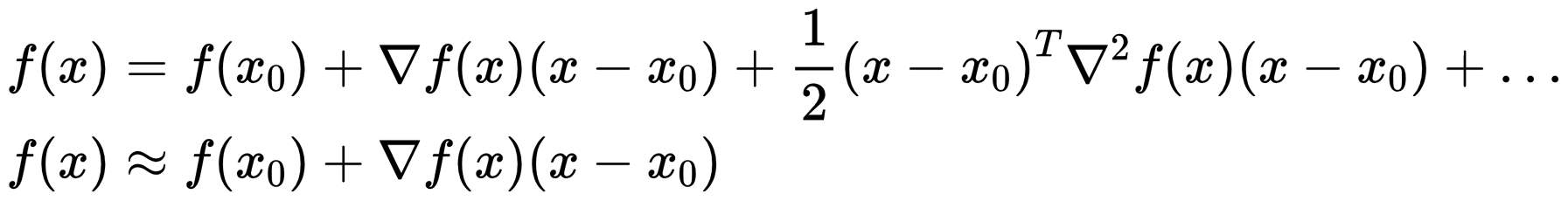
梯度下降法认为梯度的反方向就是下降最快的方向,所以每次将变量沿着梯度的反方向移动一定距离,目标函数便会逐渐减小,最终达到最小。
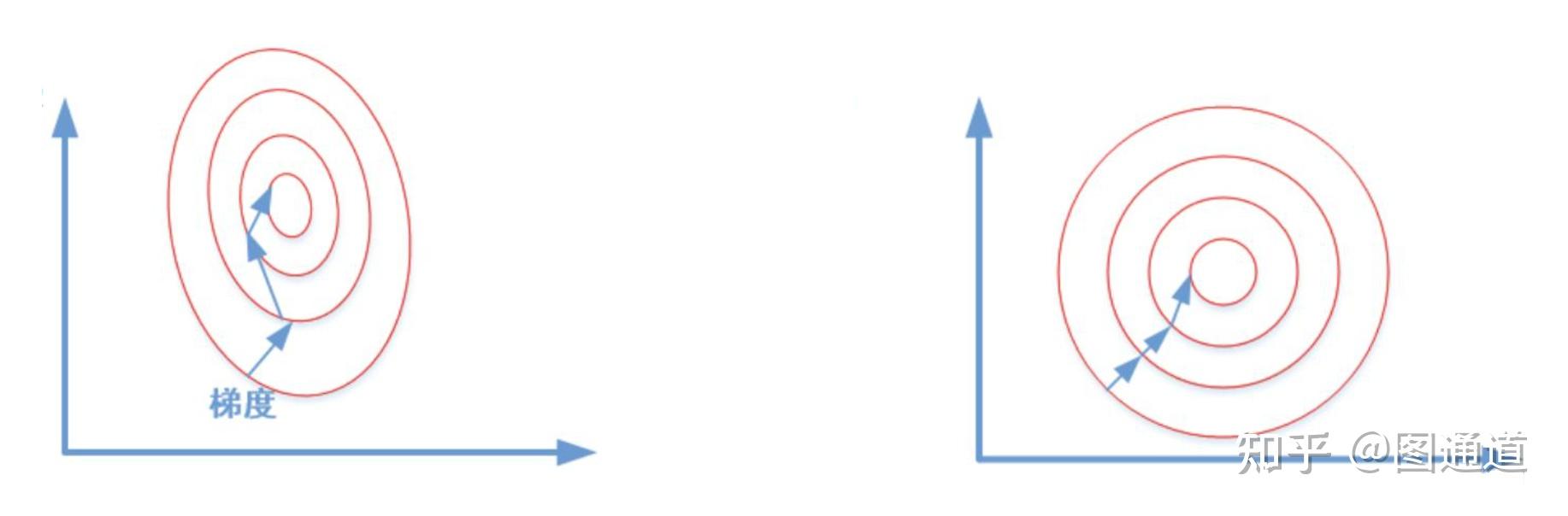
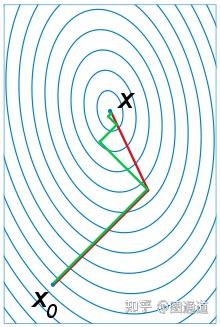
当目标函数是凸函数时,梯度下降法的解是全局最优解。其它一般情况下,不保证是全局最优解。虽然在局部的搜素方向是最快下降方向,但从整体来看,梯度下降法的整体速度也未必是最快的。形象一点来说:如果在X1点以梯度方向到X2点,X2点以梯度方向到X3点,可能不是X1点到X3点的最佳路径。 这一点在接近局部最优解时体现的尤为明显:
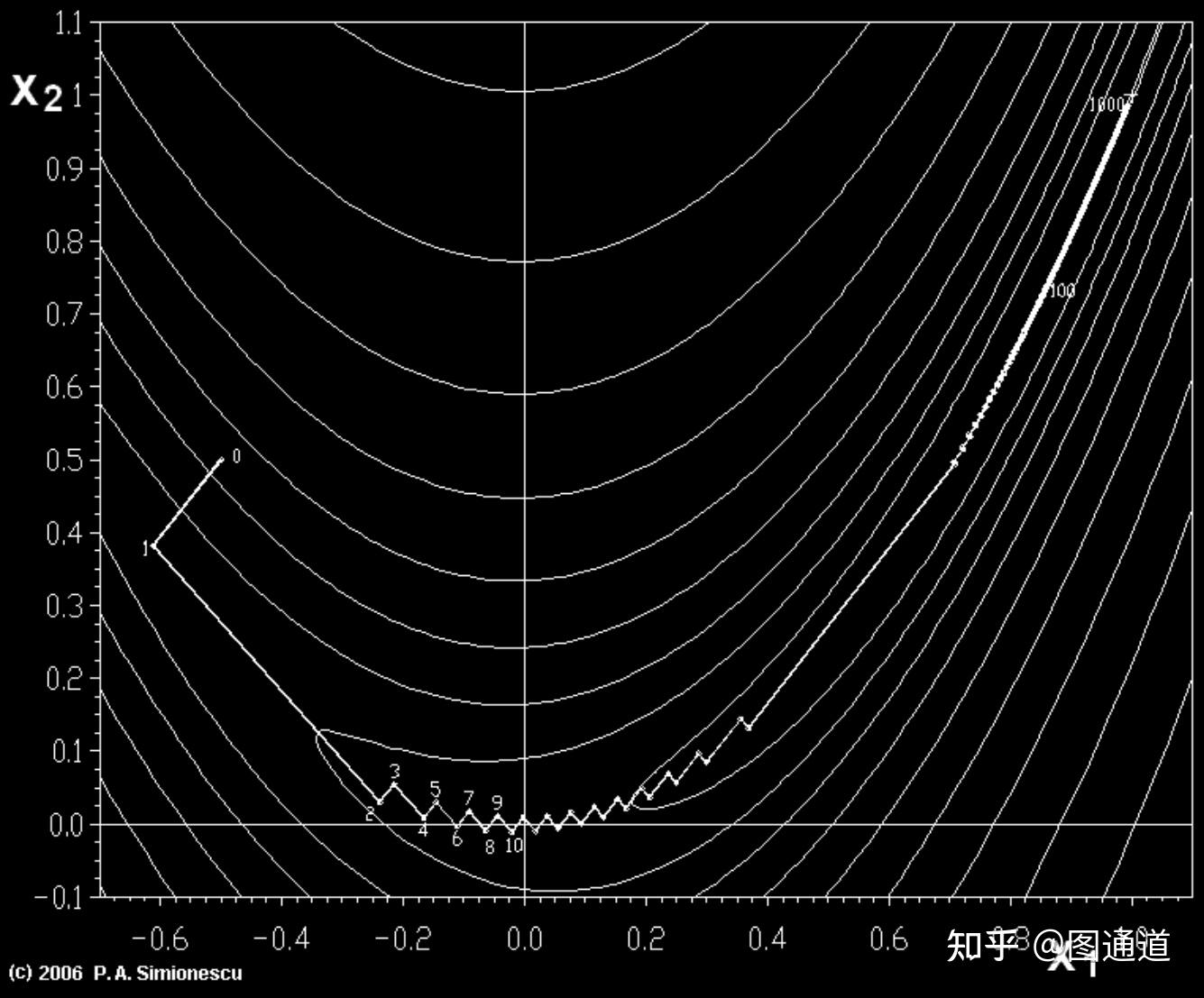
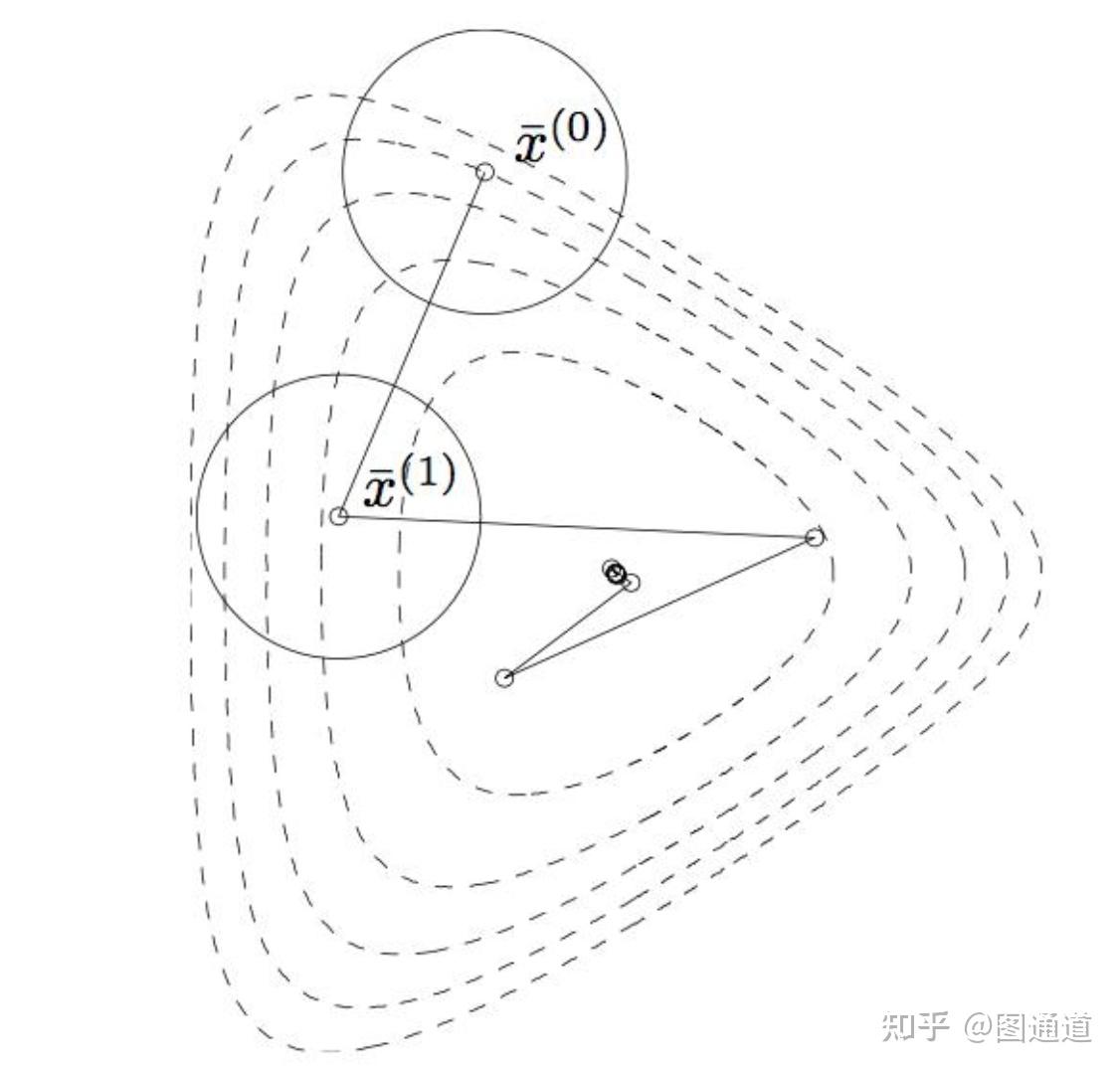
- 靠近极小值时收敛速度减慢
- 可能会“之字形”地下降
那么问题来了,梯度下降法和最速下降法有什么区别呢?其实没啥区别,很多时候会混用这两个名词。在应用上述梯度下降法的时候提到了下降方向,但是光有方向还不够,还需要有步长,梯度下降法通常会假设一个步长a,对每一步都采用同样的步长。
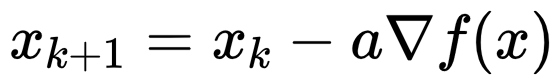
最速下降法的步长都是求解一个一维问题(关于步长的)来确定的,相当于在一个优化问题了嵌套了一个求解最优步长的优化问题,本质上没有区别。
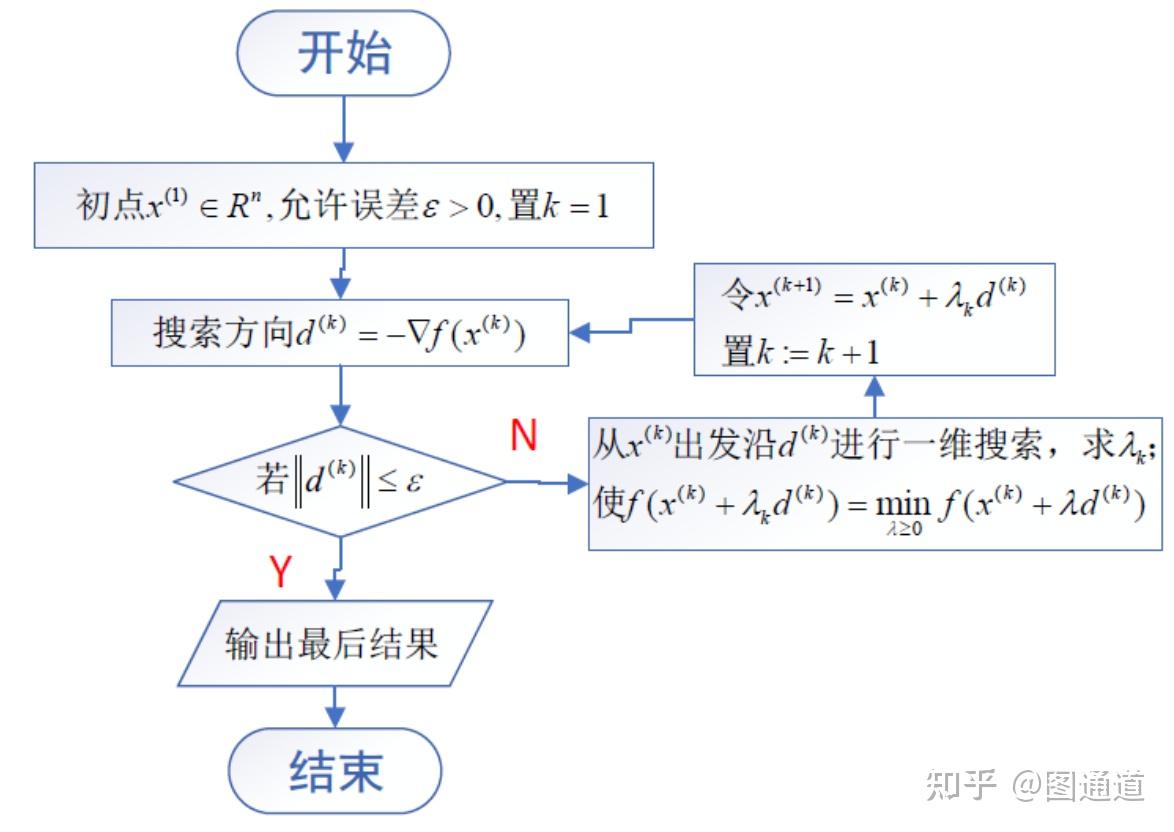
下面我们来看一个梯度下降法的例子:
求解下列无约束优化问题的梯度下降法
f=@(x1,x2) x1.^2 + x1.*x2 + 3*x2.^2;
初始点 x0=[3 3]

% 梯度下降算法部分代码:
while and(gnorm>=tol, and(niter <=maxiter, dx >=dxmin))
% 计算梯度:
g=grad(x);
gnorm=norm(g);
% 步长:
xnew=x - alpha*g/gnorm;
xnew=x - alpha*g;
% 检查步长
if ~isfinite(xnew)
display(['迭代数: ' num2str(niter)])
error('x不合理')
end
% 绘制当前迭代
if k==1
pause(6)
end
k=k+1
plot([x(1) xnew(1)],[x(2) xnew(2)],'w*-')
pause(.1)
niter=niter + 1;
dx=norm(xnew-x);
x=xnew;
end在机器学习中,为了更好的解决上述遇到的问题,发展了两种梯度方法的变体,有兴趣的可以自行研究一下:
- 批量梯度下降---最小化所有训练样本的损失函数,使得最终求解的是全局的最优解,即求解的参数是使得风险函数最小,但是对于大规模样本问题效率低下。
- 随机梯度下降---最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近,适用于大规模训练样本情况。
总体来说,梯度方法有如下优势:
- 时间复杂度低,在每一个迭代中,只需要计算梯度,不需要对二阶导数矩阵(即海森矩阵(Hessian Matrix))进行计算。(下文将提到的牛顿法及其变体耗费了大量代价计算
海森矩阵)
- 空间复杂度低,因为梯度向量为一个n×1的向量,比起
海森矩阵来,占用存储空间小n倍。
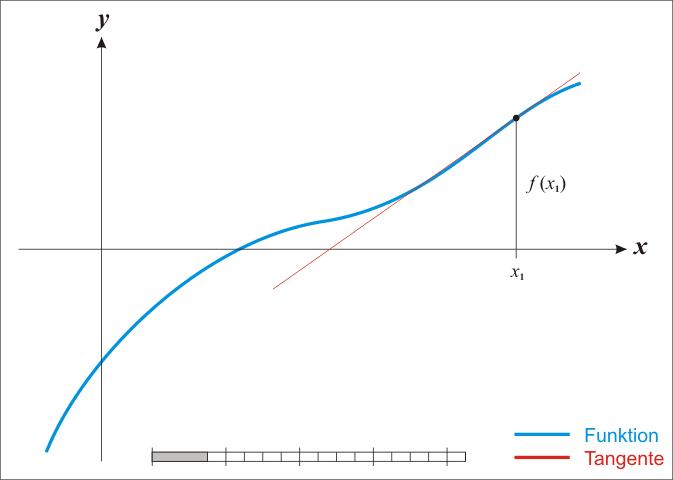
牛顿法也是一种迭代格式,如下公式所示。除了需要求解梯度外,还需要求解二阶导数矩阵(H)及其逆矩阵。
具体的推导此处就不赘述了,原理不复杂,主要用到泰勒二阶展开。
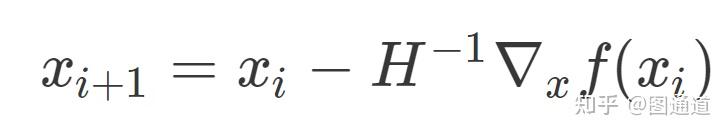
相比于梯度方法,牛顿法是二阶收敛的,所以速度快很多。通俗讲:比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。
但牛顿法的缺点也非常明显,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
因此发展了很多牛顿法的变体——简化或者替代H阵的求解。
- 高斯-牛顿法
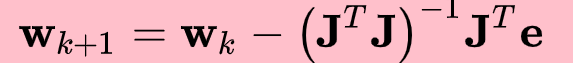
- Levenberg-Marquardt
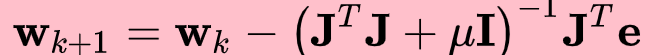
下面我们来看一个牛顿法的例子:
f=@(x)cos(x)-x;
初始点 x=-1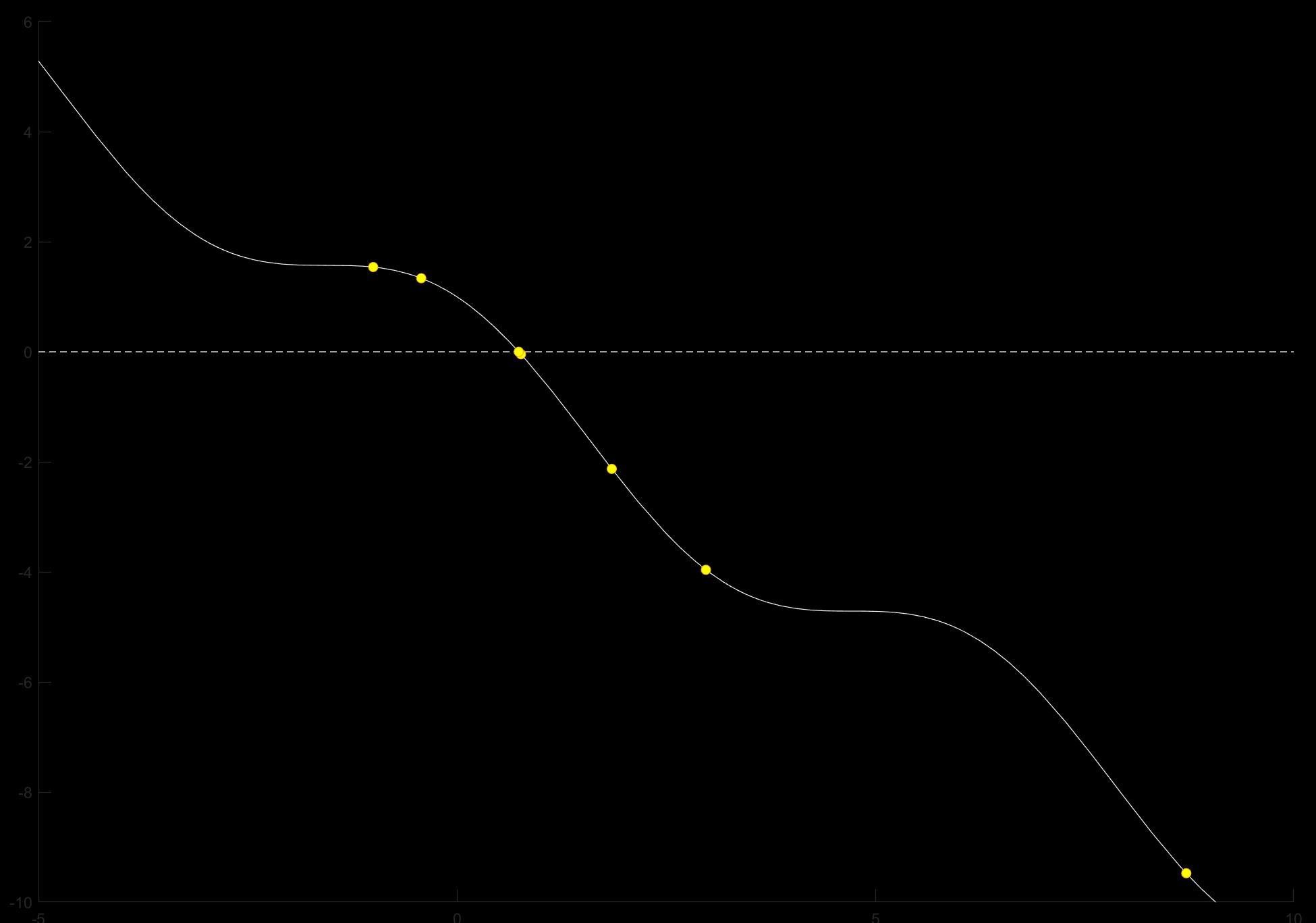
% 牛顿法部分代码
while i<=maxiter
scatter(p,f(p),'MarkerFaceColor','y');
pause(0.8)
p(i+1)=p(i)-f(p(i))/g(p(i));
FP=f(p(i));
mat(i,:)=[i p(i) FP];
if (FP==0)||(abs(p(i+1)-p(i)) < tol)
break
end
i=i+1
end对比一下梯度法和牛顿法的路径,可以发现在某些问题中,牛顿法的搜索速度要快很多。特别地,对于二次问题,牛顿法可以一步收敛。
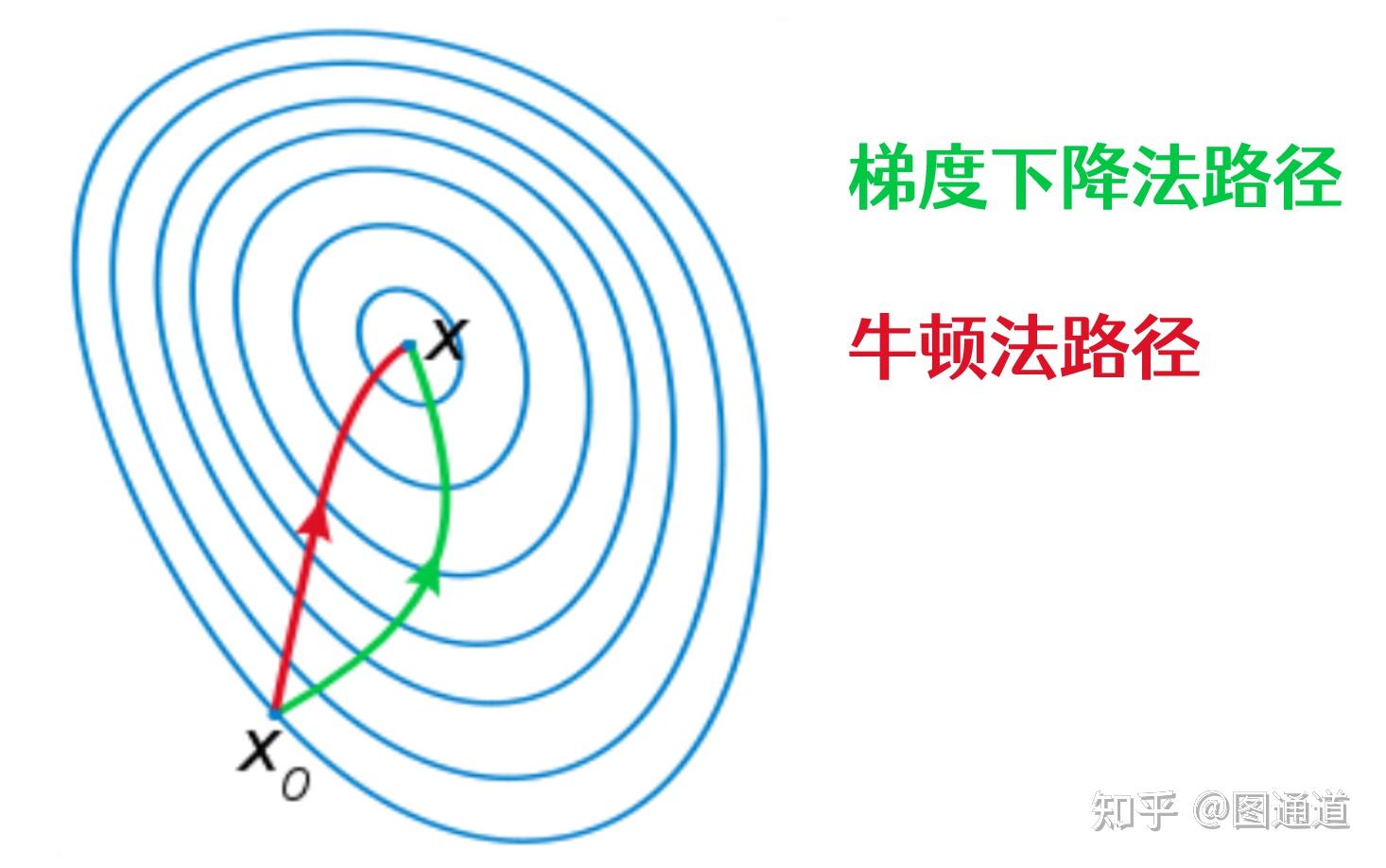
共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它
- 仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点
- 又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点
共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。 在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有“步收敛性”,稳定性高,而且不需要任何外来参数。
简单解释一下“步收敛性”,共轭梯度法最大的优势就是每个方向都走到了极致, 也即是说寻找极值的过程中绝不走曾经走过的方向,那么N维空间的函数极值也就走N步就确定了。假如是二维空间, 那就只走两步, 比最速下降法要快很多。
以上求解问题的策略都绕不开梯度,但有些目标函数是无法求解梯度的,此时就可能用到启发式方法。
启发式算法可以这样定义:一个基于直观或经验构造的算法,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解。——百度百科
现阶段,启发式算法以仿自然体算法为主,主要有粒子群算法、模拟退火法、神经网络等。

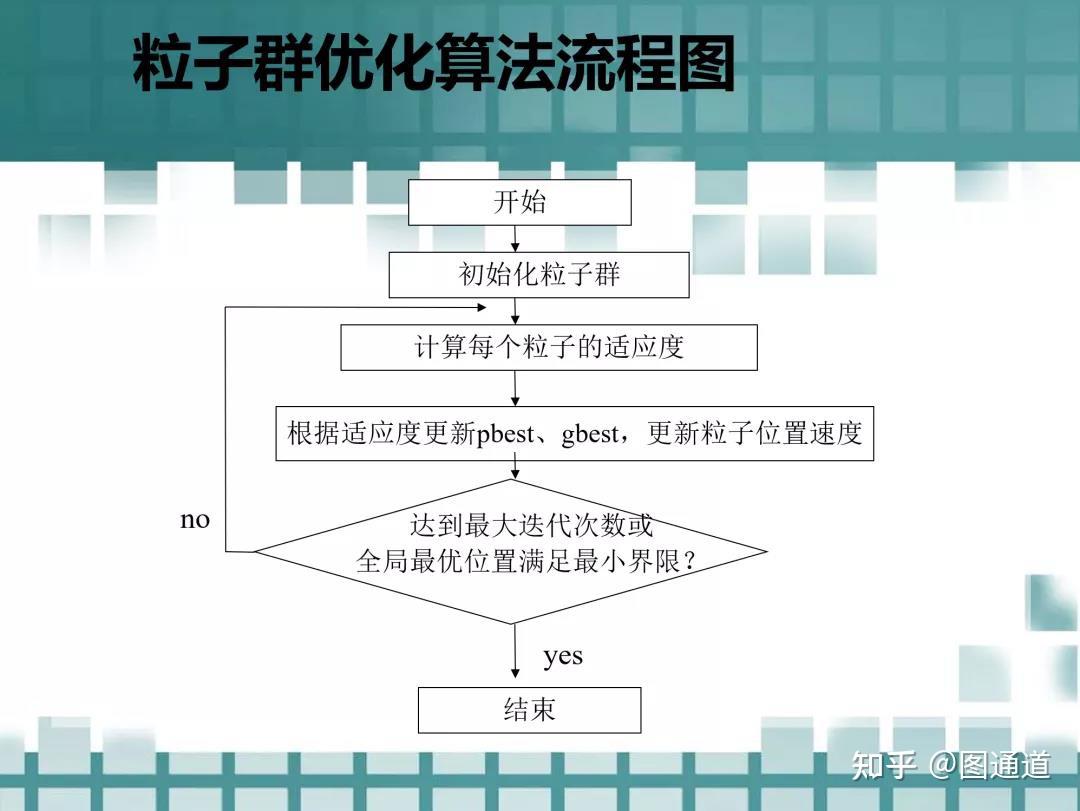
function[pglobal,value,pbest]=PSO(fitness,nPop,c1,c2,w,maxIter,Dim)
% 粒子群算法函数
% 作者:图图@图通道
% 编写时间:2021/6/24
%
% 功能说明:自行编写的基础粒子群算法函数
% 并未考虑变量的上下界,可以很容易的自行添加
% 参数说明:
%
% fitness:适应度函数,函数句柄
% nPop:粒子数目
% c1,c2:学习因子
% w:惯性权重
% maxIter:最大迭代数
% Dim:搜索空间维度
% Pi:粒子历史最优解
% pglobal:全局最优解
format long;
% 初始化种群的个体
%________________________________________________
x=rand(nPop,Dim); % 位置
v=rand(nPop,Dim); % 速度
% 计算各个粒子适应度,并初始化局部/全局最优解
%________________________________________________
plocal=x; %plocal为局部最优解
p=zeros(nPop,1); %p为局部最优值
for i=1:nPop
p(i)=fitness(x(i,:));
end
pglobal=x(nPop,:); %pglobal为全局最优解
for i=1: nPop-1
if fitness(x(i,:))<fitness(pglobal)
pglobal=x(i,:);
end
end
%进入主要循环,按照公式依次迭代
% ———————————————————
for t=1:maxIter
for i=1:nPop
% 粒子运动公式
v(i,:)=w*v(i,:)+c1*rand*(plocal(i,:)-x(i,:))+c2*rand*(pglobal-x(i,:));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:))<p(i)
p(i)=fitness(x(i,:));
plocal(i,:)=x(i,:);
end
if p(i)<fitness(pglobal)
pglobal=plocal(i,:);
end
end
pbest(t)=fitness(pglobal);
end
value=fitness(pglobal);
pglobal=pglobal';
pbest=pbest';
end完整内容可以往期文章:《粒子群算法到底有多少分身?》
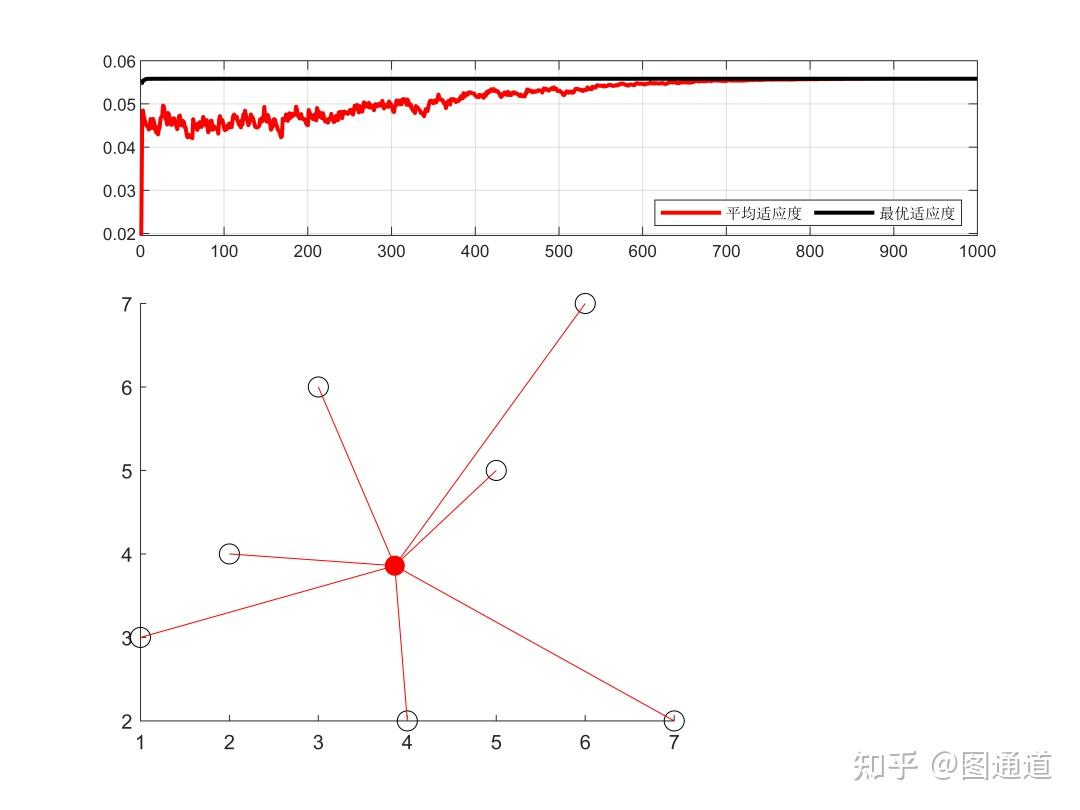
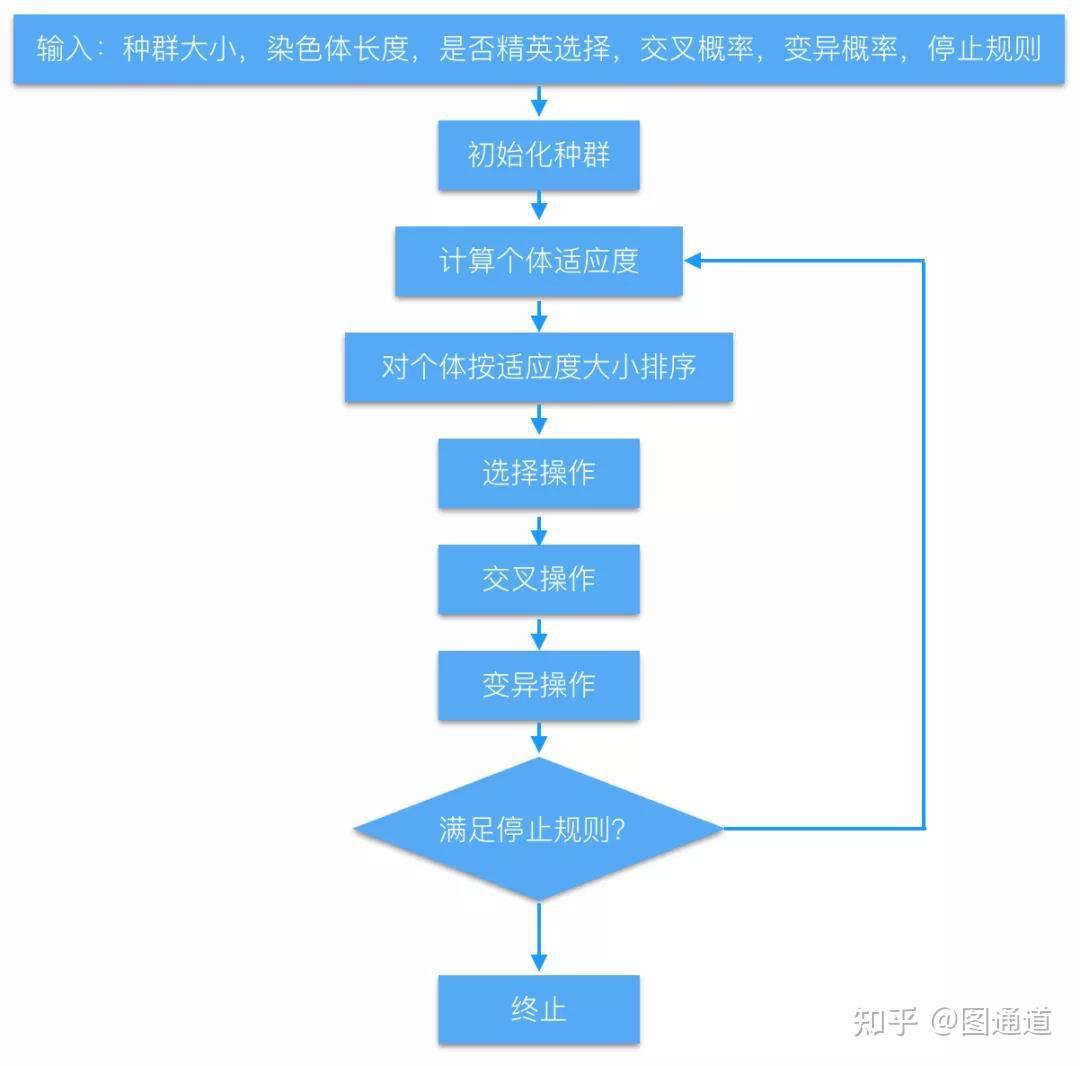
完整内容可以参考往期文章:《从细胞生物学到遗传算法(GA)》
当然还有很多启发式算法,这里就不一一列举了,在往后的推送中会具体介绍。此外,本文仅对优化/迭代算法进行了一下梳理,并没有展开讲各个算法的原理,仅希望能方便大家了解脉络,并选择适合自己问题的求解方法。具体的原理讲解,如果大家比较感兴趣【点赞=感兴趣】,后面会补充更新。
参考列表:[1]http://zhuanlan.zhihu.com/p/36902908;[2]http://www.cnblogs.com/maybe2030/p/4946256.html;[3]http://zhuanlan.zhihu.com/p/64227658;
- 需要文中所有模型代码的可以联系图图;



